L'objectif était de comprendre comment une machine peut apprendre. Pour ce, j'ai utilisé plusieurs approches.
La première s'est appuyée sur l'implémentation d'un algorithme de clustering simple, en mode non supervisé, basé sur la méthode des K-Means. Les résultats de cette approche sont très impactés par l'ordre de prise en compte des données. Il a donc fallu itérer de nombreuses fois pour trouver la meilleure solution qui permet de définir l'espèce à plus de 98%.
La seconde approche s'est appuyée sur les connaissances acquises lors de la première approche pour mettre en oeuvre un réseau neuronal. Deux implémentations de l'apprentissage ont été analysées, l'une itérative et l'autre parallèle pour construire ce réseau, avec une réflexion sur les implications de chaque approche. Quelle que soit la méthode, le réseau obtenu n'est pas impacté par l'ordre de prise en compte des données et nous permet de définir l'espèce à 100%.
La méthode parallèle peut représenter toutes les combinaisons possibles des caractéristiques des Iris en un nombre très réduit de neurones. Mais cette approche nécessite un deuxième niveau de généralisation pour mettre en évidence un schéma sous-jacent aux données.
La méthode itérative nécessite plus de neurones pour représenter toutes les combinaisons possibles des caractéristiques des Iris. Mais la représentation graphique de la structure du réseau fait apparaître un schéma sous-jacent aux données dès le premier niveau de généralisation. Ce schéma permet de définir les questions discriminantes à poser pour identifier chaque espèce et permet d'accéder à un niveau supérieur de connaissance.
Il convient de dépasser l'usage de l'IA en tant qu'outil en s'intéressant à la représentation des réseaux pour acquérir une connaissance supérieure des schémas sous-jacents présents dans nos données. Il me semble que ce peut-être une façon de comprendre et d'améliorer l'ensemble de nos processus mais aussi nos modèles sociétaux et politiques.
Nous entendons beaucoup parler d'IA ces dernières années et le moins que l'on puisse dire est que l'on entend de tout. Or il est difficile pour un néophyte comme moi, que ce soit en neurobiologie ou en algorithmie, de se faire une idée sur ce qu'est une IA comme ce que signifie apprendre, que ce soit pour nous ou pour une machine. Ce sont des concepts flous et soit on s'en accommode, soit on s'y investi pour mieux les appréhender.
Pour m'y investir, j'ai quelques alliées :
Pour cette expérience dans le monde de l'apprentissage machine, j'ai donc choisi le problème de classification des espèces d'Iris avec le jeu de données des Iris de Fisher. Il s'agit d'un petit jeu de données et d'un problème qui, selon Wikipédia, ne peut pas être résolu avec la méthode des K-Means.
J'ai donc décidé de commencer par vérifier pourquoi avant de proposer une approche et, évidemment, d'implémenter l'ensemble du code pour être sûr d'appréhender moi-même chaque partie du problème.
On part d'un ensemble de points et l'on va décider du nombre de centres de gravité que l'on souhaite. Au fur et à mesure on associe chaque point au centre de gravité qui lui est le plus proche et on recalcule la position du centre de gravité pour prendre en compte la nouvelle association. Les centres de gravité vont donc se déplacer au fur et à mesure qu'on leur associe des points. Une fois que tous les points ont été associés, on vérifie que chaque point est associé au bon centre de gravité. Si ce n'est pas le cas, on l'associe au centre de gravité le plus proche et on recalcule les deux centres de gravité (celui qui a perdu un point et celui qui en a gagné un). On s'arrête quand aucun point associé n'a été déplacé.
Cela signifie que l'on va tourner au minimum deux fois sur l'ensemble du jeu de données.
Cet algorithme est prévu pour mettre en avant des groupes de points sans savoir ce qu'ils représentent et sans forme de supervision.
Idéal est un bien grand mot (maux) mais si l'on raisonne un peu, il apparaît clairement que si l'on a autant de centres de gravité que de points, c'est comme si l'on avait appris chaque valeur par coeur. À l'opposé si l'on ne prend qu'un centre de gravité, la généralisation est maximale mais on sera incapable de conclure quoique ce soit. La réalité est nécessairement entre les deux.
Entre les deux extrêmes les positions des points vont varier en fonction du nombre de centres de gravité que l'on souhaite. Le nuage de points d'un centre va se situer autour des coordonnées du centre avec une distance minimale et maximale qui est aisément calculable. L'ensemble des points d'un centre constitue donc un volume (muti-dimensionnel car toutes les dimensions des points sont prises en compte lors du placement). Ce volume peut-être nul lorsque tous les points se trouvent au même emplacement.
On peut calculer le volume associé à une solution et le positionner sur un axe. En définissant, sur un autre axe, le nombre de centres de gravité, nous obtenons une courbe. En répétant l'opération pour un nombre de plus en plus grand de centres de gravité on note une inflexion qui donne une idée du nombre de centres de gravité "idéal" de nos données. Malheureusement les solutions dépendent de l'ordre de sélection des points. Aussi nous faut-il effectuer plusieurs calculs pour identifier une solution "acceptable". Acceptable car rien ne nous permet d'être sûr que nous disposons de la meilleure solution.
Dans la pratique l'implémentation pose rapidement des questions car les seuls exemples que l'on trouve sur Internet ne gèrent que des points avec une ou deux dimensions. Or, au delà de l'intérêt, il est rare que nos jeux de données soient limités à deux dimensions ou variables d'entrées.
Autre aspect, les exemples de code deviendraient vite complexes pour un nombre important de dimensions. Enfin, ces exemples sont dédiés à un nombre de dimension précis. Gérer un nombre variant de dimensions implique un code dynamique. Dans les librairies de code implémentant cet algorithme, les données sont généralement concaténées avant d'être envoyées, ce qui permet de palier la question du nombre de dimensions. Les limites sont, dès lors, celle de la mémoire et celle du temps de traitement.
Dans mon premier exemple, je me suis appuyé sur un jeu de données supervisé, celui des Iris (cf. Références), pour pouvoir vérifier ce que j'obtenais et en tirer des conclusions.
Ce jeu de données comporte 4 dimensions et 150 lignes. Selon l'article sur Wikipedia, il n'existe pas de solution parfaite ce qui me laisse à penser qu'il manque une dimension au jeu de données.
Pour accepter plusieurs dimensions, mon implémentation s'appuie sur des DataTable .Net. L'avantage de cet objet est que sa structure est dynamique tant en termes de colonnes que de lignes. Cela induit une limite à 1024 dimensions, ce qui est peu, dépendamment du jeu de données concerné mais largement suffisant pour celui des Iris et pour une première implémentation. Dans une seconde implémentation je pense utiliser des chaînes de caractères avec un séparateur (un format CSV en somme).
L'initialisation des centres de gravité pose également question. Je les ai initialisés sur des points sélectionnés aléatoirement. Si à l'évidence cela fonctionne, nous allons voir que ce choix n'est pas sans implication. Il y a probablement des stratégies plus heureuses. J'imagine que s'appuyer sur les résultats obtenus avec un seul centre de gravité pourraient permettre de les répartir dépendamment de la densité des points mais je n'ai pas testé cette approche.
Le fait de s'appuyer sur un jeu de données supervisé permet, une fois chaque solution calculée, de calculer son erreur et c'est là que l'on perçoit bien les implications de l'initialisation aléatoire des centres de gravité ainsi que la sélection aléatoire des points du jeu de données lors du placement. En revanche cela permet d'effectuer autant de calculs qu'on le souhaite pour trouver les meilleures solutions.
Un autre point qui pose question est le fait qu'un centre de gravité puisse ne plus être associé à aucun point. Sur 8000 calculs cela m'est arrivé une fois. C'est donc un événement rare mais pour lequel il convient de prendre une décision. J'y vois quatre options :
Pour l'instant, vu le nombre de cas, j'ai décidé de gérer les erreurs de calcul et de le laisser vide.
Le dernier point qui pose question est le calcul du volume où se situent les points d'un centre. Il y a des cas particuliers qui impactent le résultat :
Pour pouvoir effectuer des comparaisons entre les volumes calculés des solutions, j'ai décidé d'ajouter à l'algorithme la taille minimale d'un point pour chaque dimension. De cette manière, pour le jeu de données d'exemple, les volumes correspondent toujours a un calcul en cm4.
En ayant calculé des milliers de solutions, l'erreur minimale est de 1/27 sur un centre de gravité d'une solution qui en comporte 10.
Les campagnes de tests ont été menées selon la méthodologie suivante :
Un fichier agrégé comporte les colonnes suivantes :
En analysant l'ensemble des fichiers agrégés et en classant les données par erreur et nombre de centres de gravité croissants, nous pouvons voir que la solution optimale trouvée est le calcul 2976 avec 3,57% d'erreurs et 10 centres de gravité. On y trouve des solutions avec moins de centres de gravités (7 et 8) avec 6,9 % d'erreurs.
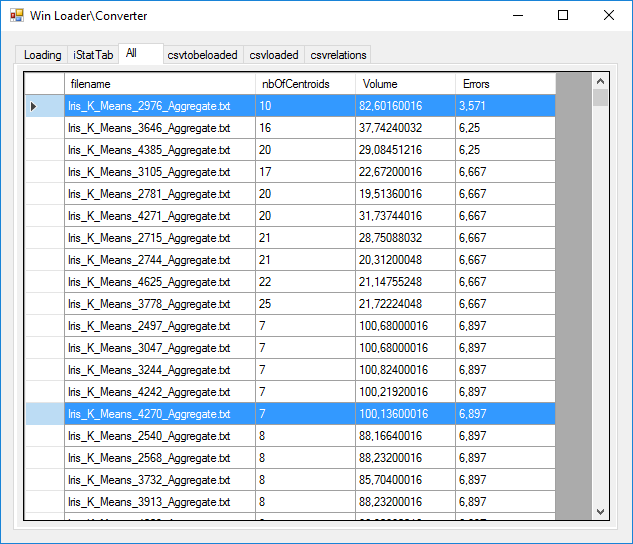
Un fichier détaillé comporte les colonnes suivantes :
Commençons par voir les données détaillées de la solution ayant le taux d'erreur le plus faible, l'itération 2976, pour la comprendre (image ci-dessous). Ce sont les lignes sélectionnées en bleu.
Comme précisée, elle comporte 10 centres de gravités (de 0 à 9). Le premier centre de gravité (0) a les coordonnées arrondies (4.98, 3.45, 1.46, 0.27). Il a fallu 4 rotations pour que les 10 centres soient stables, +1 sans rien changer (d'où la valeur de 5). Ce centre comporte 19 points associés à l'espèce "Setosa" et aucune autre espèce. Il n'y a donc aucun mélange pour ce centre de gravité (et donc aucune erreur probable).
Dans les données, nous voyons que le second centre de gravité présente un mélange d'espèces avec un Iris de type "Versicolor" et vingt-sept Iris de type "Virginica". Cela implique que l'on a un risque, si l'on place un Iris présentant des dimensions similaires, de se tromper d'espèce à raison d'1 erreur sur 27 (d'où les 3.571%).
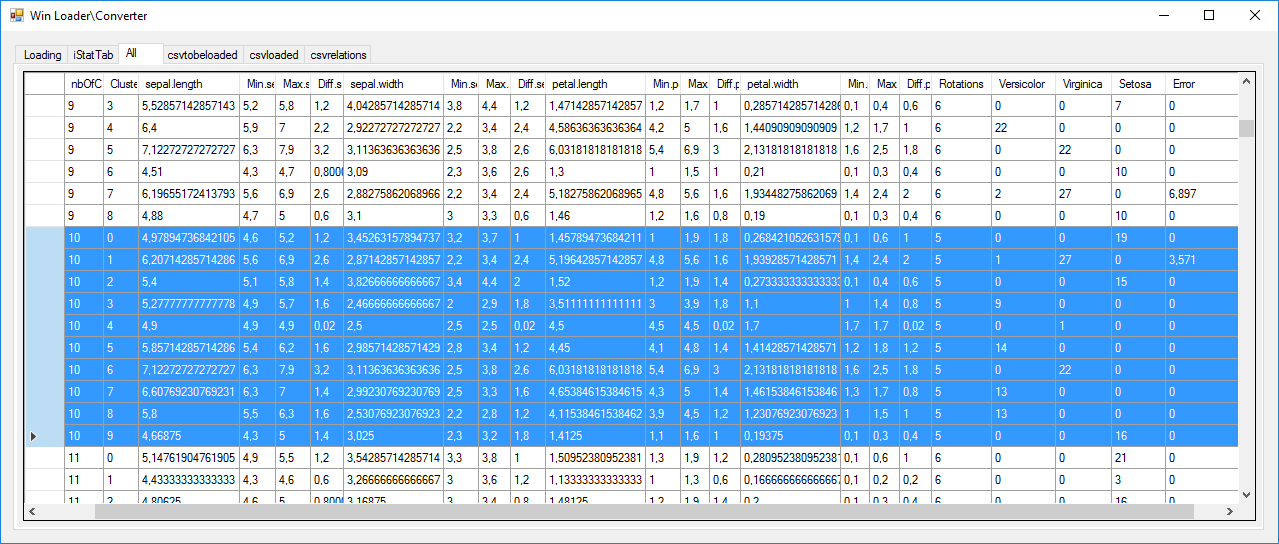
Le cinquième centre de gravité (le 4) présente le cas particulier de ne disposer que d'un Iris de type "Virginica". Il s'agit d'un cas "appris par coeur".
Nous retrouvons nos 150 fleurs sur le tableau avec chaque espèce associée à plusieurs centres de gravité dépendamment des dimensions possibles de ses sépales et pétales.
Continuons avec la solution ayant 7 centres de gravités, l'itération 4270, pour la comprendre (image ci-dessous). Ce sont les lignes sélectionnées en bleu.
Cette fois, il nous a fallu une rotation de plus pour obtenir une solution stable (5+1). Nous retrouvons une solution "apprise par coeur" (celle associée au troisième centre de gravité [le 2]). Nous avons, cette fois, 2 risques d'erreur sur 27, d'où le pourcentage d'erreur de 6.9%. Autre point remarquable, cette fois les 50 Iris "Setosa" ne sont servis que par un seul centre de gravité.
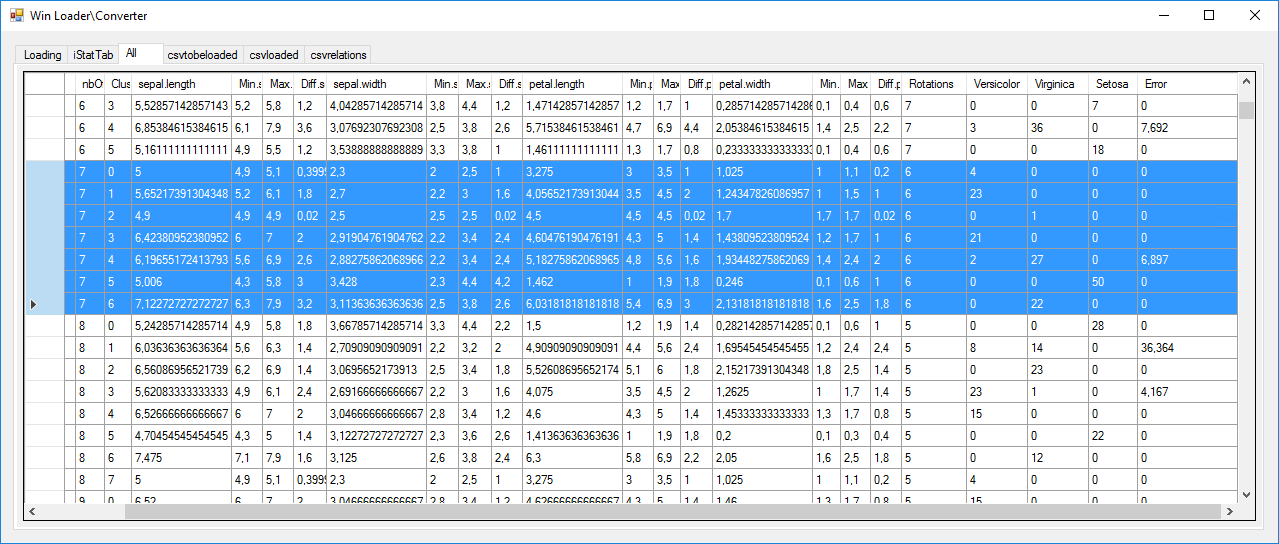
Comme précisé sur Wikipédia, après plus de 20 000 calculs, il semble qu'il n'y ait pas de solution parfaite avec l'usage de l'algorithme K-Means pour ce jeu de données. Dans le meilleur des cas, nous avons 1 erreur sur 27 et une solution apprise par coeur. Malgré tout cela m'a permis d'implémenter l'algorithme, de comprendre son usage et ses problématiques, d'y apporter des réponses et d'exploiter ses résultats. Enfin, ces résultats et cette compréhension devraient me permettre de franchir la seconde étape qui est d'essayer de répondre au même problème mais, cette fois, en utilisant des neurones numériques.
Généralement un réseau de neurones est structuré et entraîné sur la moitié des données puis vérifié sur l'autre moitié.
J'avoue ne pas être "fan" de cette approche en deux phases car elle ne correspond pas à la réalité biologique. Notre cerveau se restructure en permanence en fonction de nos apprentissages. Je vais donc partir d'un réseau vierge en ajoutant, au gré des données, des neurones ou en corrigeant les seuils de déclenchement et d'inhibition et remonter des informations sur l'efficacité de l'approche.
Théoriquement, une telle approche n'a pas de limite tant en termes d'entrées que de sorties. Cela signifie que si l'on souhaitait y ajouter d'autres apprentissages, il suffirait d'ajouter un nouvel ensemble de neurones. Le principal inconvénient que j'y vois est le maintien en opérationnel d'un grand réseau pour rien. On peut faire plus intelligent avec un chargement dynamique des réseaux en fonction des entrées\sorties nécessaires mais cela sort du cadre de cet article.
Est-ce que cela veut dire qu'un ensemble de neurones seraient dédiés à une expertise ?
Cela me semble crédible pour les neurones de sortie et pour la logique de l'expertise mais pas pour les entrées. Les valeurs dimensionnelles des pétales peuvent être les variables d'entrée de beaucoup de fleurs par exemple.
Il me semble donc que des variables d'entrée peuvent être intégrées à plusieurs réseaux d'expertises à la condition, bien sûr, que les unités des données restent les mêmes. Cela implique de normaliser les données avant mise en oeuvre et apprentissage d'un réseau. Dans le cas du jeu de données des Iris, celles-ci sont en centimètre ce qui ne correspond pas vraiment au standard International ....
Dans le convertisseur analogique/numérique j'ai construit et défini les seuils manuellement. J'aurai pu créer un générateur pour n'importe quelle conversion et précision mais je n'y ai pas trouvé d'intérêt particulier.
L'idée, ici, est de construire et régler les seuils au fur et à mesure de l'injection des données.
Que savons-nous pour l'instant ?
Chaque centre de gravité dispose de quatre dimensions d'entrée. Pour chaque dimension nous avons un ensemble de points répartis de part et d'autre de la valeur du centre, sur un segment identifié. Nous allons "remplacer" ce segment par un neurone (en vert sur le schéma ci-dessous) n'ayant qu'une dendrite et dont les seuils d'activation et d'inhibition correspondent aux valeurs du segment concerné. Ces neurones servent d'entrée mais surtout de filtre pour les valeurs autorisées, sur chaque dimension, pour un centre de gravité donné.
Pour un centre de gravité, j'ai donc besoin de quatre de ces neurones d'entrée. Ceux-ci vont être connectés à un neurone principal correspondant au centre de gravité (en jaune sur le schéma ci-dessous). Celui-ci n'est censé être activé que lorsque ses quatre entrées sont activées et là, la structure de mes neurones pose problème. En effet ils n'ont aucun moyen de savoir quelles entrées sont activées et encore moins de savoir si elles sont toutes activées car ils réagissent à des seuils d'activation et d'inhibition. Or, dépendamment des valeurs d'entrée d'une dimension, je pourrais dépasser le seuil d'activation sans que les quatre neurones d'entrée ne soient tous actifs.
Mes neurones ont été conçus pour une valeur de sortie dépendante de la somme des valeurs d'entrée. En somme, leur sortie "Y = AX" ou "X" est la somme des valeurs d'entrées et "A" un paramètre de réduction\amplification. En électronique, ils fonctionnent un peu comme des transistors en mode amplification. Or les transistors sont également largement utilisés en mode commutation et c'est là où réside la solution. Je vais donc faire évoluer mes neurones pour obtenir "Y = AX + B". Ainsi, si je veux dissocier le signal de sortie d'un neurone de la somme de ses entrées, il me suffit de définir "A=0" et fournir, à "B", la valeur de sortie souhaitée. Rien de plus facile donc et cela me semble en phase avec le biologique.
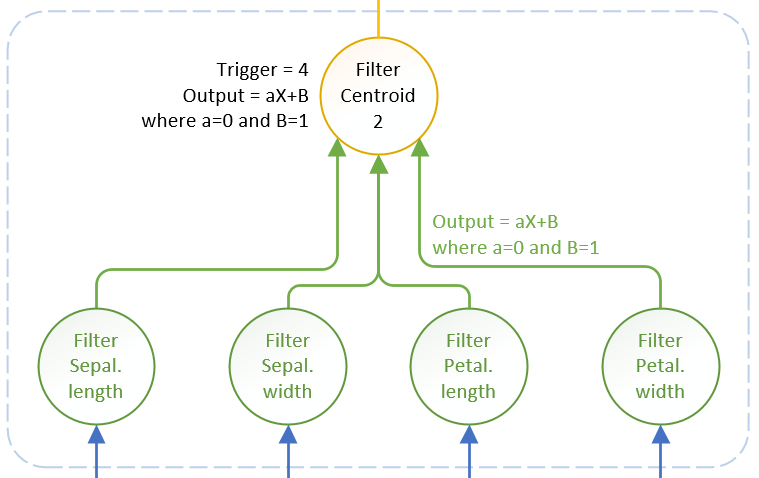
Mes neurones d'entrée vont donc avoir une valeur de sortie de "1" lorsqu'ils sont actifs, indépendamment de leur valeur d'entrée. Le neurone suivant ne sera activé que pour un seuil de "4" ... simple en somme et nous voici avec une fonction booléenne "AND".
En même temps, cela a un sens car un expert raisonne avec des graphes de décisions constitués d'expressions booléenne (vraies ou fausses).
Le neurone d'un centre de gravité va fonctionner de la même manière et sortir 1 lorsqu'il a identifié une espèce.
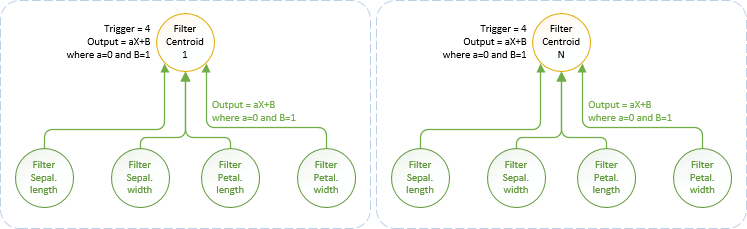
Nous avons vu avec le "K-Means" que nous pouvions avoir plus d'un centre de gravité pour une même espèce. Notre réseau va donc être constitué d'un ensemble de "blocs" neuronaux qu'il va falloir alimenter en données d'entrée et vérifier en sortie. Cela nécessite un peu de réflexion quant à la gestion et la forme de ces entrées\sorties.
Quel peut-être l'environnement d'un réseau expert ? Il peut être seul, hébergé au coeur d'une application métier spécifique, comme il peut faire partie d'un ensemble plus vaste de réseaux.
Dans le second cas, chaque réseau est dédié à une expertise spécifique mais, chacun peut partager toute ou partie de ses entrées et de ses sorties avec d'autres. Les termes "entrées/sorties" ne me semblent pas particulièrement adaptés dans la mesure ou les sorties peuvent être vues comme les entrées d'autres réseaux. Il s'agit tout au plus de points de données (que je vais donc appeler des "DataPoints"). Ces "DataPoints" sont vus comme une ressource au niveau de l'ensemble des réseaux et, chaque réseau peut y faire référence pour en faire soit des entrées, soit des sorties. Ainsi, par exemple, il serait possible de rassembler les caractéristiques des fleurs et de les associer à une matière médicale. Il faut, évidemment un brin de gouvernance pour ces "DataPoints" en les référençant dans une taxonomie associée à l'ensemble des réseaux. Cette taxonomie doit comporter, pour chaque "DataPoint", à minima, l'expression de ce qu'il représente, son type de donnée et son unité.
Autre aspect, comment définir ces réseaux au regard de l'ensemble et les construire ?
Celui des Iris est simple et pourrait se définir ainsi : Expert("Iris.Species", Variety = Sepal.length AND Sepal.width AND Petal.length AND Petal.width). Voici comment interpréter cette expression:
Dans le cas des "Iris", nous avons un réseau "plat" constitué de quatre entrées et d'un neurone les reliant et associé à une espèce d'Iris. Nous aurions pu avoir un cas plus complexe avec, par exemple, une expression booléenne comme Variety = (Sepal.length AND Sepal.width) OR (Petal.length AND Petal.width) En pareil cas, nous aurions un neurone pour chaque bloc booléen, relié à deux entrées et un neurone final, reliant les neurones des blocs et associé à une espèce d'Iris. L'expression booléenne est fondamentale car elle représente la structure de base d'un réseau expert.
L'image ci-dessous montre les implications sur la structuration du réseau dépendamment des deux expressions Booléennes. Le "OR" est défini par le "trigger=1" impliquant qu'un seul bloc sous-jacent est nécessaire pour activer une espèce. Le "AND" est défini, comme nous l'avons vu précédemment, par le "trigger=2" ou "4" dépendamment du nombre d'entrées qui doivent être activées.
L'expression ne fait que définir la forme de base du réseau expert. Le réseau final dépend des règles d'apprentissage, et donc de son optimisation ou, dit autrement, ce qui a été "compris", lors de sa construction.
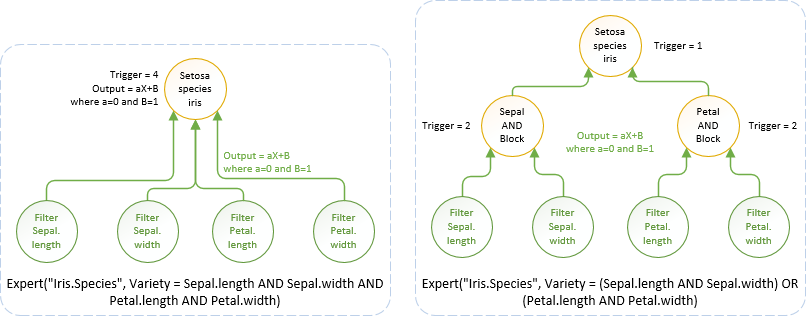
Avant de pouvoir envoyer des données à un réseau, il nous faut le déterminer au niveau de l'ensemble des réseaux. Nous allons donc lui envoyer l'expression qui le caractérise (ici: Expert("Iris.Species", Variety = Sepal.length AND Sepal.width AND Petal.length AND Petal.width)). Cela doit avoir pour conséquence de déclarer ces entrées\sorties dans l'ensemble des réseaux, si elles n'existent pas. Nous pouvons noter que notre expression ne comporte pas les unités des entrées\sorties. Cela implique soit que notre expression est trop simple soit qu'il nous faut référencer les unités dans une seconde étape et par un autre moyen.
Le jeu de données peut avoir une structure différente, auquel cas, il faut préciser les règles de correspondance entre les noms et, si les données ne sont pas exprimées dans les mêmes unités, il faut les convertir avant de les envoyer au réseau. Si une correspondance de noms est simple à définir, la conversion entre unités peut être plus complexe et peut nécessiter du code spécifique. Au niveau de l'ensemble des réseaux, nous pouvons estimer que les données reçues doivent respecter et les règles de nommage et les unités. Cela déplace le problème sur le fournisseur des données et simplifie la solution.
L'étape suivante consiste à envoyer les données au modèle et à lire ses sorties. Les données d'entrée doivent être fournies à tous les neurones d'entrée du réseau et les valeurs de sorties doivent être lues sur tous les neurones caractérisant les espèces d'Iris. Pour faire simple, nous allons associer les neurones correspondants aux entrées\sorties.
Lors de l'envoi de la première ligne de données, il n'y aura aucun neurone associé ni aux entrées ni aux sorties et donc aucune réaction possible. "Pas de réaction" peut vouloir dire plusieurs choses et, en fonction, des actions spécifiques sont nécessaires :
Pour m'aider dans les choix, je vais fournir aux neurones une capacité évènementielle lorsqu'ils atteignent un certain seuil. Nous savons lorsqu'ils sont activés car cela est nécessaire pour que le signal se propage sur le réseau mais rien ne me précise, pour l'instant, s'il sont à, mettons, 80% de leur seuil d'activation ou 20% de dépassement. Ce point peut être précieux pour identifier les neurones à corriger et éviter d'avoir à parcourir systématiquement tous les neurones d'une espèce. J'entrevoies d'autres applications à un tel mécanisme évènementiel comme la mise en oeuvre d'une forme d'intuition ... mais nous verrons cela plus tard.
Cela m'amène à une réflexion à la fois technique et philosophique.
La nature s'est organisée au fur et à mesure de l'évolution et les données que nous en obtenons comportent forcément des aspects de ces organisations. L'usage d'algorithmes de classification, par exemple, fait émerger une part de ces organisations. Mais attention au choix des données utilisées.
Si l'on s'intéresse à la façon de structurer ces données, dans des bases de données, dans un modèle normalisé, nous aurions des structures pour chaque dimension et une structure centrale les reliant et représentant les espèces. Classiquement nous lions les données entre elles par leurs identifiants. Ces identifiants sont des valeurs numériques, généralement auto-incrémentées, commençant à 1. Elles ne définissent que l'ordre d'insertion des données dans la base de données. Le sens qu'elles portent est donc limité à cet ordre.
Dans la structure neuronale, les dimensions sont reliées par leur valeur et non par des identifiants. Ce point est fondamental car le sens porté par les identifiants est très éloigné de celui des valeurs. Relier les identifiants serait perdre l'organisation portée par les valeurs des données.
La généralisation peut certainement prendre des formes très différentes en fonction de la nature des données. Avec le K-Means, par exemple, nos centres de gravité ont été associés aux valeurs dimensionnelles de sépales et pétales. Les coordonnées d'un centre de gravité est une généralisation qui fait émerger une organisation des données. C'est en ce sens que c'est un algorithme "intelligent". Au niveau technique, la relation entre un centre de gravité et ses points s'est faite sur l'identifiant de chaque ligne du jeu de données. Si cela permet d'économiser de la mémoire, ce lien n'est que technique et n'apporte que peu de sens.
Rien n'empêche d'utiliser des données techniques pour une généralisation, à la condition, j'imagine, que la valeur de ces identifiants uniques évolue au gré de l'évolution de la compréhension. La seule chose qu'on leur demande est de rester unique mais rien n'empêche de faire en sorte qu'il porte une forme d'organisation. Avec le K-Means, par exemple, nous aurions pu, lorsque l'on associe un point à un centre de gravité, changer son identifiant pour représenter cette association et porter une information de distance par rapport au centre par exemple. Une telle pratique pourrait permettre d'obtenir simplement tous les points les plus proches ou les plus éloignés d'un centre de gravité par exemple.
Attention donc au sens porté par nos données et donc à utiliser les "bonnes" données pour alimenter nos réseaux.
Un "fait" est constitué d'observables et détermine un résultat. Dans notre cas, les observables sont les données d'entrée et le résultat la variété d'Iris. La logique qui s'applique aux données d'entrée permet de déterminer le résultat. Le jeu de données comporte donc 150 faits.
L'ensemble des faits constitue une connaissance.
Raisonner est lorsqu'on fournit une partie des valeurs des observables et que ces valeurs se trouvent dans les écarts attendus. La logique ne permet pas d'obtenir un fait mais une probabilité de faits. Cela permet, par exemple, d'obtenir les variétés probables pour une longueur de pétale donnée. Une amélioration consiterait à accepter des expressions pour les valeurs des observables (l'équivalent d'une clause "Where" en langage "SQL"). Le raisonnement pourrait être "renforcé" par "l'usage" en conservant les demandes faites au réseau et les résultats obtenus. Ce renforcement pourrait pondérer les résultats d'un raisonnement mais cela pourrait également créer un biais lié à l'usage en supprimant une partie de l'objectivité.
L'intuition est proche du raisonnement sinon que toutes ou partie des valeurs des observables ne se trouvent plus dans les écarts attendus mais dans une proximité définie avec ces écarts. Si la valeur de cette proximité peut-être globalement appliquée à tous les écarts, elle peut être très réduite lors de la construction du réseau pour des valeurs très proches mais contradictoires en termes de résultat.
En somme, si raisonner peut exprimer une certitude ("au regard des données, c'est telle ou telle variété à x%"), l'intuition ne peut s'exprimer qu'au conditionnel ("Au regard des données, cela pourrait être telle ou telle variété à x%").
En classant, par ordre décroissant, les probabilités issues du raisonnement et de l'intuition, et en sélectionnant les plus fortes, nous pouvons orienter une décision lorsque nous ne disposons pas de toutes les valeurs des observables. Si cela ne fournit pas de fait, au delà de l'orientation, cela permet de préciser ce que ce n'est pas.
Les résultats du K-means sont intéressants. Chaque centre de gravité, pour chaque dimension, dispose d'un ensemble de points qui se répartissent dans un segment. Je n'ai pas regardé si cette répartition correspond à un schéma particulier mais cela a certainement un sens. J'ai donc créer un objet neurone activable non pas sur une valeur mais sur un segment.
La structure neuronale est définie par une équation booléenne des plus simples. La sortie, une espèce d'Iris, est activée lorsque les quatre dimensions d'entrées sont activées (largeurs et longueurs des pétales et sépales). Le neurone de sortie étant activé par un seuil comment sait-il qu'il est activé par les quatre dimensions d'entrée ? S'il est relié qu'à quatre neurones, chacun étant lié à une dimension précise, la question ne se pose pas, mais que se passe t'il dans le cadre d'une boucle de contre-réaction ou si l'on multiplie les neurones d'entrées ? Il ne le sait pas, tout simplement. Mais alors, comment garantir qu'il va être activé que dans des conditions précises ? Je ne vais pas répondre à toutes les questions car il faut bien que je vous laisse quelques réflexions mais il est clair que l'algorithme d'apprentissage joue une rôle sur ce point :)
Pour revenir à notre problème, il y a plusieurs approches algorithmiques. Il en existe au moins deux, l'une itérative et l'autre parallèle.
Intéressons d'abord à l'approche parallèle pour mieux comprendre certaines problématiques. Nous pouvons séparer le jeux de données par espèce d'Iris et construire un réseau dédié indépendamment. Puisqu'il y a trois espèces, nous allons obtenir trois jeux de cinq neurones (quatre en entrées et un en sortie pour l'espèce concernée). Si l'ensemble des données d'entrée fournissent une seule espèce en sortie, nous pourrions nous arrêter là. Apprendre les cent cinquante solutions par coeur aurait nécessité six cents neurones. Avec cette approche, nous en avons quinze et si l'outil répond à nos questions correctement, que demander de mieux ?
Nous pouvons faire beaucoup mieux avec un second niveau de généralisation et effectuant une comparaisons des segments d'activation des neurones d'entrée. Pourquoi le faire ? Parce que cette seconde généralisation nous amène, par la main, vers une compréhension plus fine d'un schéma sous-jacents de nos données.
Je n'ai pas construit la solution parallèle car je ne l'ai perçue que dans un second temps, en m'interrogeant sur l'optimisation de l'approche itérative. C'est celle-ci que j'ai construite et c'est une chance car elle a fait ressortir un schéma sous-jacents de nos données dès le premier niveau de généralisation. Et c'est en représentant les résultats que j'ai compris que l'algorithme ne faisait que révéler un schéma présent dans les données. Cette représentation est la suivante :
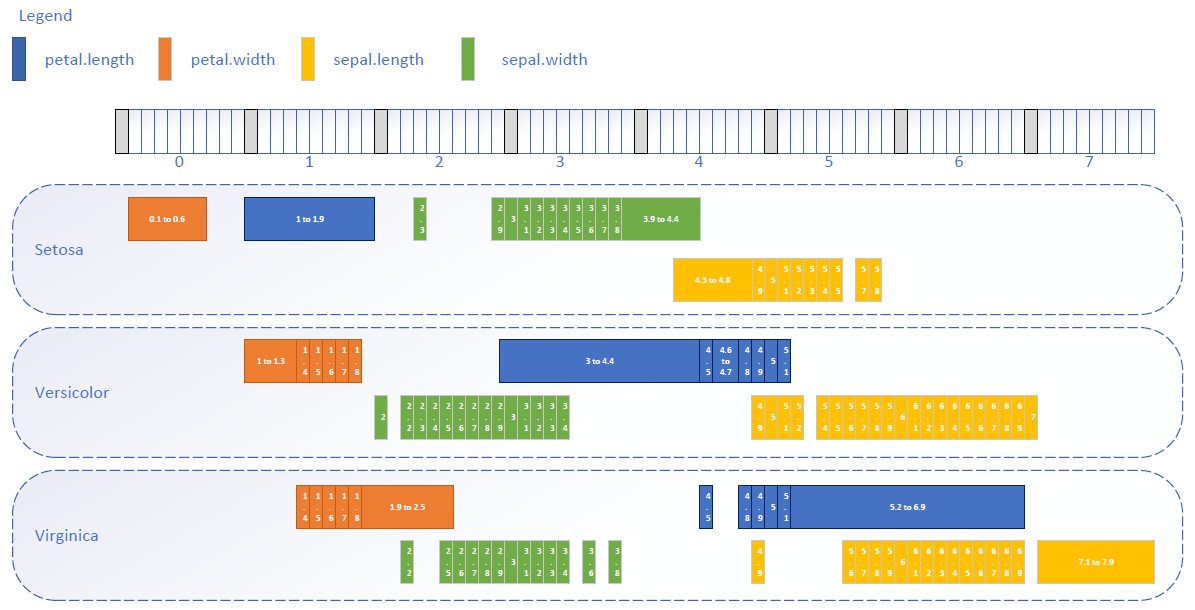
Chaque rectangle correspond à un neurone. Chacun est activé sur un segment de valeurs ou, à minima, sur une seule valeur. Chaque bloc en pointillé correspond à une espèce et donc au neurone de sortie. Dans le cas présent, il n'y a pas de neurones intermédiaires mais s'il y en avait, leur représentation pourrait avoir de l'importance pour mieux interpréter les schémas sous-jacents de nos données.
A partir de la taille des segments d'activation nous pouvons définir et ordonner les questions à poser. Nous en revenons à ce qu'un expert ferait par expérience sinon qu'ici, le jeux de questions et leur ordre dépend de l'analyse du schéma et donc de la structure du réseau à la fin de son apprentissage. A l'évidence la longueur des pétales et la première des questions à poser car elle est la plus discriminante, sauf pour les valeurs de 4,5 cm et entre 4, 8 et 5,1 cm. Pour toutes autres valeurs, elle permet de déterminer une espèce ou l'absence de conclusion. Si elle n'est pas suffisante, la largeur des pétales peut-être demandée ensuite. Cette largeur couvre une "surface" d'activation moindre que la longueur mais elle est discriminante pour toutes valeurs sauf entre 1,4 et 1,8 cm. Cette représentation pourrait être enrichie de la densité des points pour créer des couleurs plus ou moins vives et restituer une idée de la densité des données. Cela représenterait un paysage de nos données avec des montagnes (les plus fortes densité), des plateaux et de vallées (les moins fortes densités).
Si nous en étions resté au premier niveau de généralisation de l'algorithme parallèle, nous aurions dû demander toutes les dimensions pour pouvoir conclure sur l'espèce. On touche du doigt à quel point les représentations d'un réseau et l'analyse de ces représentations est fondamentale pour atteindre un autre niveau de connaissance. Évidemment avec des données, des réseaux et des algorithmes plus complexes, l'interprétation des paysages représentés et l'exploitation de la structure des réseaux peuvent représenter un défi mais cela est fondamental pour dépasser le simple usage de l'outil. Face à une trop forte complexité d'interprétation, à minima nous pouvons comparer les paysages obtenus dans des situations différentes. Ce pourrait être la comparaison d'une politique dans différents pays par exemple. L'analyse des différences entre ces situations par des experts devraient nous permettre de mieux interpréter ce que représentent une montagne, un plateau et une vallée dans le cas concerné et d'orienter nos décisions.
Est-ce qu'il faut analyser nos données avec des algorithmes d'IA ? Oui, pour mieux comprendre les schémas sous-jacents de nos données. Cette approche pourrait bien nous mener à un autre niveau de connaissance et civilisationnel.
Est-ce que cela peut impacter notre enseignement ? Il me semble dèsormais que l'approche algorithmique est fondamentale et qu'elle doit être enseignée dès le plus jeune âge pour développer des compétences dans la représentation et la critique de celles-ci. Il nous faut apprendre à arpenter les chemins et plus seulement regarder la destination.
Est-ce qu'il nous faut implémenter nous-même ces algorithmes ? Je pense que oui car leur implémentation nous permet de les comprendre, d'être critiques sur leurs approches, sur les résultats et sur les représentations possibles et leurs interprétations. En aucune manière nous ne devons rester à l'usage d'algorithmes programmés par d'autres et accessibles sous forme de services qu'ils exposent. Cela représenterait un risque stratégique.
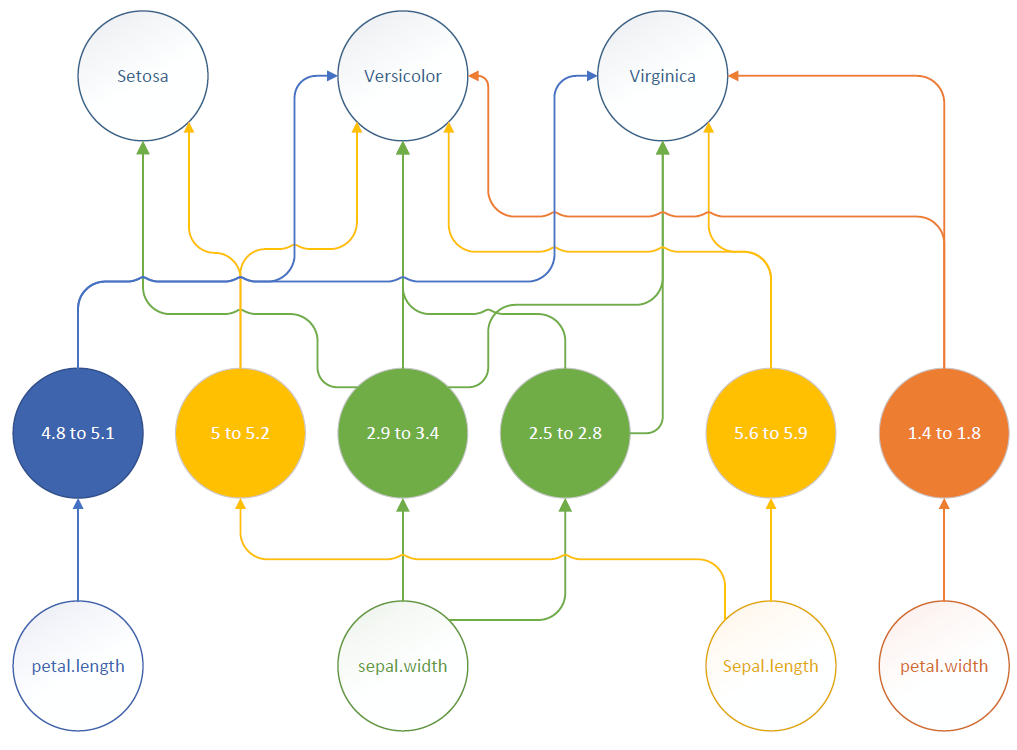
Quelles sont les prochaines étapes quant à ce travail ? Implémenter un second niveau de généralisation selon le modèle imagé ci-dessous. Cela va avoir pour conséquence de réduire le nombre de neurones de la solution itérative ou d'augmenter le nombre de neurones de la solution parallèle. Dans les deux cas, le résultat obtenu sera le même sinon que la solution parallèle sera plus simple et plus performante, ce qui oriente sérieusement le choix. Je vais également ajouter des sorties non plus binaires mais probabilistes pour pouvoir intégrer les notions de raisonnement et d'intuition. En outre, il me semble évident que les entrées et les sorties peuvent être réutilisées par d'autres réseaux. Il me faudrait donc des données d'autres espèces de fleurs pour pouvoir chaîner des réseaux spécifiques entre eux à partir des mêmes dimensions d'entrée notamment. Enfin, mon approche et l'algorithme est limité a des cas précis. S'ils sont adaptés à des réseaux expert, il ne peuvent pas faire de la reconnaissance d'images par exemple car, à l'évidence, l'équation de la reconnaissance d'images n'est pas une équation booléenne et il me semble que les neurones d'entrée doivent effectuer une soustraction et non être activés sur un segment ... Bref cette descente dans le monde des algorithmes m'a tout l'air de m'amener comme Alice, dans le terrier d'un lapin ...
Dans cet article je me suis intéressé à deux approches différentes de mise en oeuvre d'un modèle expert. L'objectif initial était d'essayer de répondre à la problématique en m'appuyant sur un algorithme non supervisé qui est le K-Means et, dans un second temps, en construisant un réseau neuronal dynamiquement.
Comme toujours je suis parti d'une approche naïve, sans m'appuyer sur un Framework quelconque et sans apprentissage particulier sur le domaine concerné. L'objectif est d'être le plus critique possible, de comprendre les problèmes au fur et à mesure, d'y répondre par analyse et de les implémenter car seule l'implémentation prouve que les approches fonctionnent et permettent de mettre en évidence toutes les problématiques et de les comprendre finement.
Ce travail m'a apporté beaucoup avec une compréhension plus fine de ce qu'est l'IA. C'est un outil incroyable mais si nous en restons à l'usage de l'outil, à mon sens nous passons à côté de l'essentiel.
De ma compréhension actuelle, nos données reflètent des réalités dont les constructions nous échappent jusqu'à ce qu'on les analyse, les modélise pour en construire une connaissance et que l'on forme des experts. Il me semble qu'un expert est une personne qui a acquit une connaissance et, gràce à son expérience, a développé une hiérarchie fine des questions à poser afin de disposer des données qui lui sont nécessaires pour répondre à un problème particulier. Notre approche de la formation est de disséminer ces modèles et cette connaissance mais peu de personnes font le chemin de bout en bout. Or, si la destination d'un chemin peut-être une fin en soi, l'arpenter comporte bien des enseignements.
Mais quel est le lien avec l'IA ? Je dirai que chaque algorithme d'IA est un outil capable de révéler et exploiter une partie des schémas sous-jacents qui se trouvent dans nos données. Le premier résultat est un outil capable de répondre à un ensemble de questions pour y apporter des réponses. Mais l'analyse des schémas sous-jacents peut nous apporter bien plus et notamment nous permettre de hiérarchiser les questions qu'il convient de poser pour mieux y répondre et sans avoir besoin de toutes les données d'entrée. En ce sens, accéder aux schémas sous-jacents peut nous permettre d'accéder à un niveau d'expertise bien plus vite qu'un humain ne peut le faire.
Si nous en restons là, de tels algorithmes peuvent faire peur mais, comme toute crise, la peur laissera place au rejet, puis à une forme de dépression, à l'acceptation et à l'innovation pour rebondir plus haut qu'initialement. L'essentiel est de définir une trajectoire d'exploitation de ces schémas et d'expliquer cette trajectoire aux audiences concernées.
Faut-il mettre en pause la recherche sur l'IA ? Certainement pas ! Faut-il travailler sur l'IA et la compréhension des schémas sous-jacents ? Absolument ! Ne pas le faire serait se rendre dépendants d'outils développés par d'autres, accessibles sous forme de services, et qui représentent, de fait, non pas un risque mais une certitude stratégique. A défaut de les comprendre, nous devons au moins les représenter et comparer les paysages obtenus pour mettre en évidence des faits et décider d'améliorations. C'est, à mon sens, la voie pour une évolution civilisationnelle.