En cours ...
Dans cet article, nous allons nous intéresser à ce qui peut être simplifié et parallélisé pour obtenir davantage de maintenabilité et de performance. Nous allons également essayer d'aller plus loin dans nos réflexions pour améliorer notre compréhension du sujet.
Nous allons partir de la représentation graphique du réseau neuronal de la précédente étude, obtenue après un premier niveau de généralisation. Cette représentation a été, pour moi, la source de nombreuses réflexions. L'une d'elles est la transformation sous forme mathématique de cette représentation.
Pour bien comprendre, on part de la représentation graphique du réseau neuronal, après la généralisation de premier niveau, dans l'image ci-dessous, à gauche. On ne s'intéresse, ici qu'à la largeur des pétales, pour simplifier la compréhension mais, évidemment, l'approche est la même pour toutes les dimensions. La généralisation de premier niveau démontre que si la largeur des pétales est incluse entre :
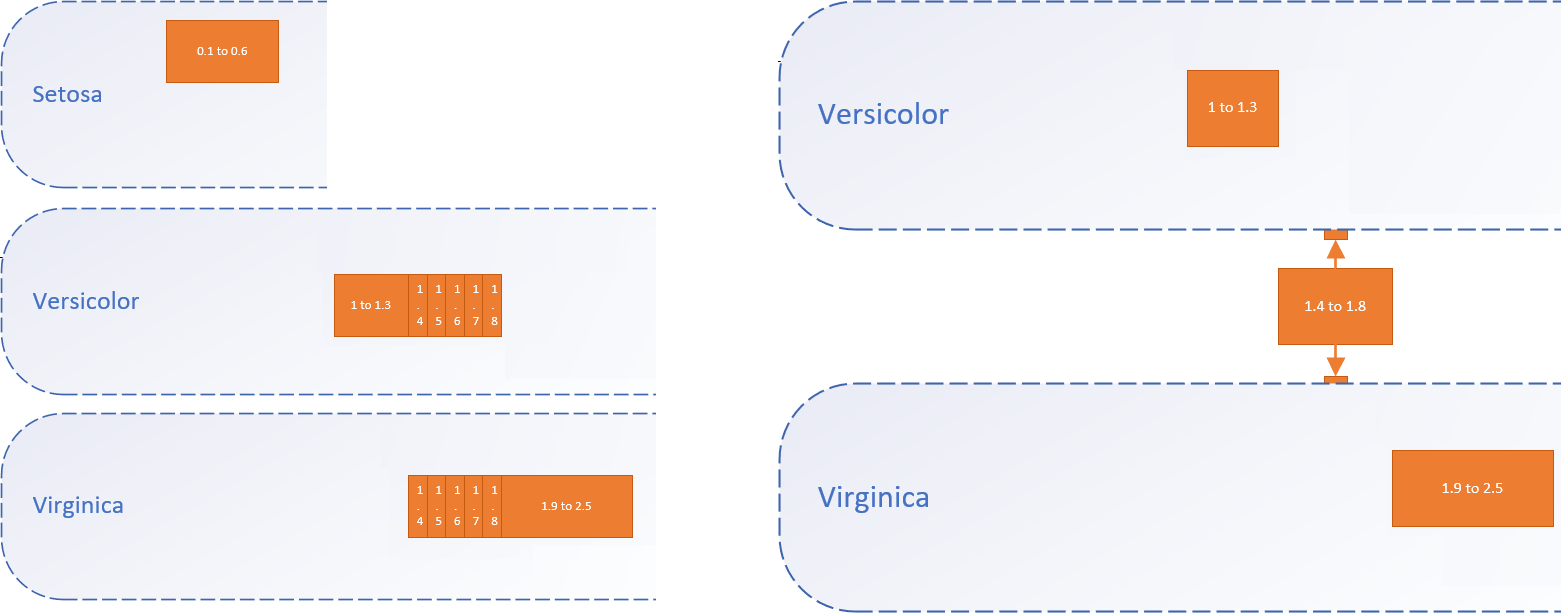
Cette énumération peut être convertie en une fonction écrite en un langage de programmation quelconque. De manière intelligible cela donne : Fonction IrisPetalWidth1(Entrée [= largeur des pétales en cm])
En language de programmation C#, par exemple, nous aurions le code suivant. On déclare une liste des espèces (notée "IrisOutput"). Comme pour la version "intelligible", la fonction "IrisPetalWidth1" prend en paramètre une valeur décimale (appelée "input") et retourne, en fonction des tests une liste d'espèces. Comme précisé en commentaire, cette liste peut être vide si la valeur d'entrée ne correspond à aucune espèce ou comporter une ou plusieurs espèces.
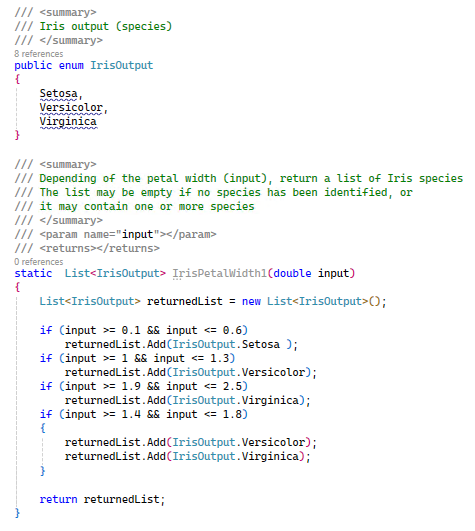
On peut ainsi créer, à partir des résultats du second niveau de généralisation, une fonction par dimension. Ces fonctions étant complètement indépendantes, elles peuvent être invoquées en parallèle, que ce soit au sein d'un même ordinateur ou d'une ferme d'ordinateurs. Cette indépendance revient au "OU" de l'expression de la structure du réseau neuronal que nous avons vu dans l'étude précédente. Évidemment il nous manque le "ET" car ce sont les résultats des quatre dimensions qui permettent de prendre une décision et non une seule.
Toutefois l'approche peut fournir un résultat même si une seule dimension est fournie. Même si une seule dimension ne suffit pas à préciser à 100% que c'est telle ou telle espèce, cela fournit une réponse probabiliste telle que "c'est telle espèce à x%".
Malgré tout, cette approche comporte plusieurs défauts parmi lesquels :
En regroupant les observations (par largeurs de pétales et par espèces), en les traçant ainsi que leurs tendances polynomiale (d'ordre 2), nous obtenons l'image ci-dessous. Nous avons également prolongé les tendances jusqu'aux axes (x = largeur des pétales, y = nombre d'observation(s)) afin d'obtenir une représentation plus claire du comportement des équations près des axes.
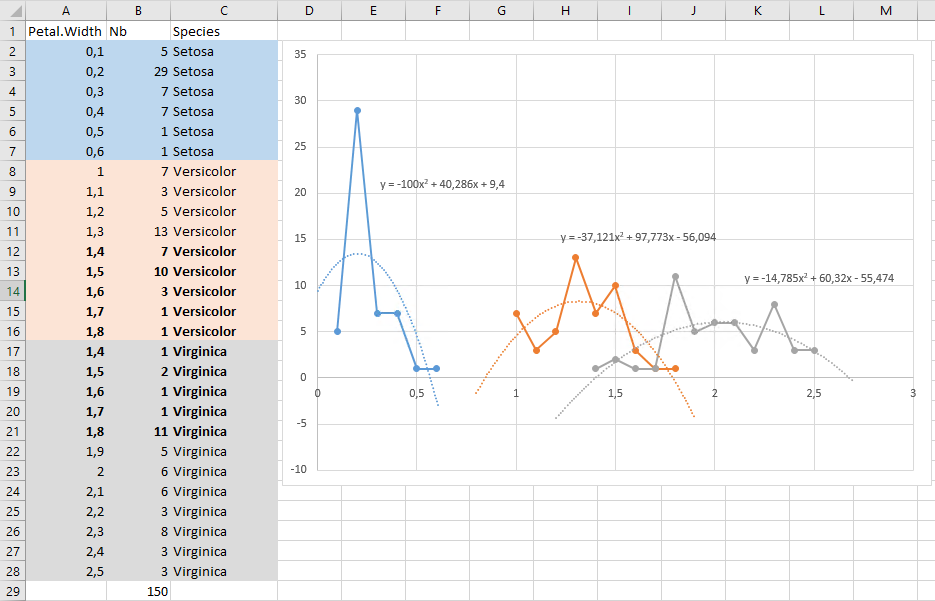
Selon les données, pour une dimension de :
Une autre question peut avoir de l'importance : Que se passe t'il si je demande l'espèce pour une valeur de 1.75 cm ? Cette valeur n'existe pas dans le tableau mais la valeur d'entrée acceptée étant une valeur décimale, une telle question peut être posée. Par raisonnement, on s'attendrait à une réponse prenant en compte les deux lignes de résultat ci-dessous :
Une autre approche, pour ce type de cas, serait d'utiliser les équations des tendances pour définir le nombre probable d'observation(s) pour une largeur donnée des pétales. Il semble évident que le type de tendance doit être le même pour une dimension et pour toutes les espèces concernées pour être sûr de comparer les valeurs d'une manière homogène. Une question se pose sur le calcul de la tendance : Quel doit être son "ordre" ? Autrement dit, est que la courbe doit être au plus proche des points observés ou peut-elle en être très éloignée et ne représenter qu'une "tendance" des points ? Ce point est traité dans le paragraphe "Approximation entre les points observés". Quelle que soit l'approche, il convient d'être consistant dans la méthode utilisée pour toute la dimension.
Normalement nous sommes censés nous appuyer sur les tendances que sur l'écart entre 1,4 et 1,8 cm inclus (pour la largeur des pétales) car c'est le seul écart ou l'on retourne plusieurs espèces. Malgré tout, il semble évident que tous les écarts peuvent être remplacés par les équations des tendances pour déterminer les espèces de sortie et leurs proportions respectives en cas de sortie multiple. L'approche est peu complexe et se passe complètement de l'approche de généralisation que nous avons suivi. Il suffit de regrouper les données par dimensions et espèces et de calculer les équations des tendances (cela implique évidemment du code pour les calculer). Ci-dessous se trouve, en exemple, à quoi ressemblerait la fonction de calcul des largeurs de pétales, en C#.
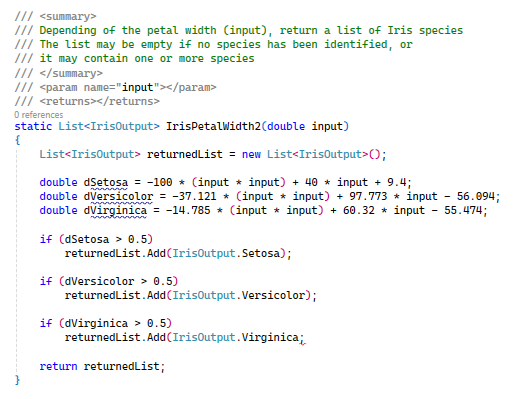
Cette approche, bien que simple, générique et efficace, présente un défaut majeur : nous perdons le schéma sous-jacent aux données. Cela implique que nous perdons de la hauteur sur les données et donc de l'expertise et nous ne sommes plus à même de définir les questions et leur ordre (par pertinence décroissante). Attention donc à ne pas tomber dans la simplicité en se suffisant des tendances et donc d'un outil.
Idéalement, il semble qu'il faille :
Cela va impliquer un remaniement de la fonction gérant la largeur des pétales. Il va notamment falloir disposer du tableau des observations regroupées par largeurs et espèces pour pouvoir préciser si une largeur d'entrée est une observation. Cela met en évidence que ce tableau peut-être très important dépendamment du jeu de données. Ce tableau est statique (tant que l'on n'ajoute pas de nouvelles données à notre modèle) et va devoir être chargé en mémoire. Dépendamment de son volume, il va impacter les ressources consommées et le temps de chargement de la solution. Dans le pire des scénarii, il pourrait empêcher le chargement en mémoire de la solution (si elle excède 2 Go par exemple). En pareille extrémité, nous n'aurions pas d'autre choix que de perdre le fait de savoir si une donnée est issue d'une observation ou non.
L'image ci-dessous correspond au code implémenté pour la gestion de la largeur des pétales.
Le code, à droite de la ligne verticale verte, correspond à l'équivalent du tableau Excel. Il regroupe toutes les observations utilisées lors de l'apprentissage, agrégées par largeur de pétales et d'espèces. Ce sont des données qui permettent de préciser, lorsque l'on utilise l'algorithme, si le résultat a été observé ou non.
Le code, à droite de la ligne verticale violette, correspond à l'équivalent d'une ligne du tableau Excel.
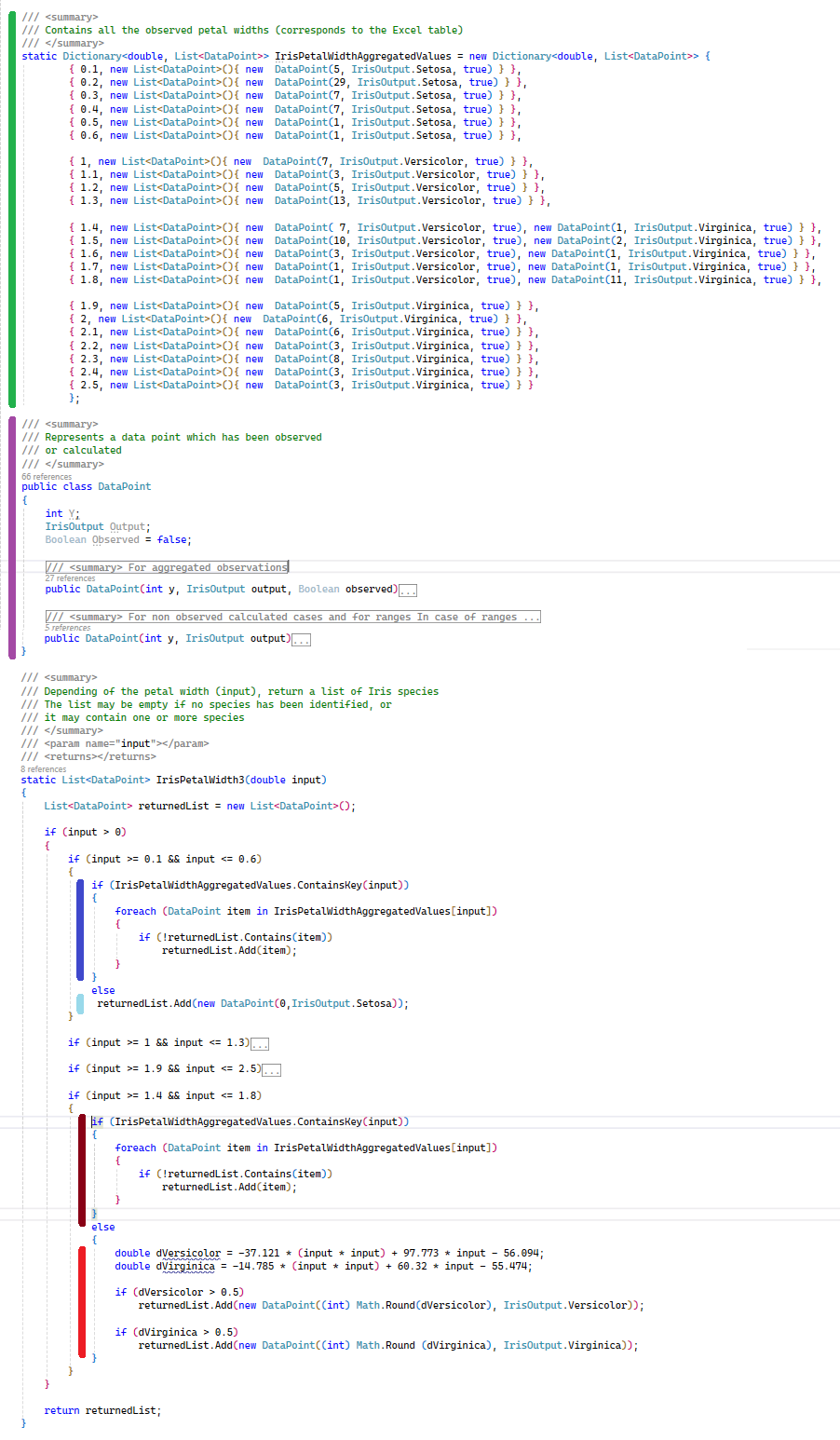
Le code, à droite des lignes verticales bleue foncée et claire, correspond à un écart ne restituant qu'une seule espèce. Dans le cas concerné, il s'agit de Setosa. Le bleu foncé correspond à un cas observé, le bleu clair à un cas non observé. Dans ce cas, le nombre d'observation est de zéro. J'ai réduit le code des écarts 1 à 1,3 et 1,9 à 2,5 car ils sont identiques en tout point sinon qu'ils restituent chacun une autre espèce. Les afficher aurait créer plus de confusion pour rien.
Le code, à droite des lignes verticales rouge foncée et claire, correspond à un écart restituant plus d'une espèce. Dans le cas concerné, il s'agit de Versicolor et Virginica. Le rouge foncé correspond à des cas observés, le rouge clair à des cas non observés. Dans ce cas, le nombre d'observation(s) est calculé en s'appuyant sur les équations des tendances.
En effectuant quelques tests nous obtenons les résultats pour les largeurs de pétales suivantes :
À ce stade nous disposons d'un code fonctionnel qui remplit l'ensemble des objectifs. Évidemment, il faut en faire de même avec les autres dimensions.
Un point qu'il convient de préciser : tout ce code ne va pas écrit manuellement. Une fois que nous avons déterminé l'approche et que l'on dispose d'un exemple concret de code, il est facile d'en faire une application qui va :
Avant tout, mettons en contexte les données. Sur nos courbes, l'axe des ordonnées correspond au nombre d'occurrence(s) d'une dimension observée. Les valeurs de cet axe sont donc des unités. Sur les abscisses nous retrouvons les dimensions mesurées de largeurs et longueurs de pétales et sépales. Ces mesures ont été faites par une personne et rien n'est précisé quant à l'outil qui a été utilisé ni concernant sa précision (du moins sur Wikipédia). Malgré tout, les dimensions fournies sont au millimètre. Prévoir une approche mathématique qui fournirait des réponses au-delà du demi millimètre ne semble pas avoir vraiment de sens. Le calcul d'un nombre d'occurrence(s) pour une largeur donnée va donc être arrondi à l'unité la plus proche.
Prévoir une probabilité pour une dimension ne semble pas être compliqué mais quelle est la probabilité que cette prévision soit juste ? Si l'on compare notre tendance polynomiale d'ordre 2 avec les observables, on voit bien qu'on est éloigné de la réalité. La courbe ne touche que 4 points pour les Virginica, même en prenant en compte les arrondis. Si l'on demande à Excel de calculer les tendances, pour les Virginica, pour des ordres supérieurs, on voit bien que la courbe tend à s'approcher de plus en plus des points observés mais également qu'il va falloir augmenter l'ordre de manière conséquente pour qu'elle corresponde à la réalité.
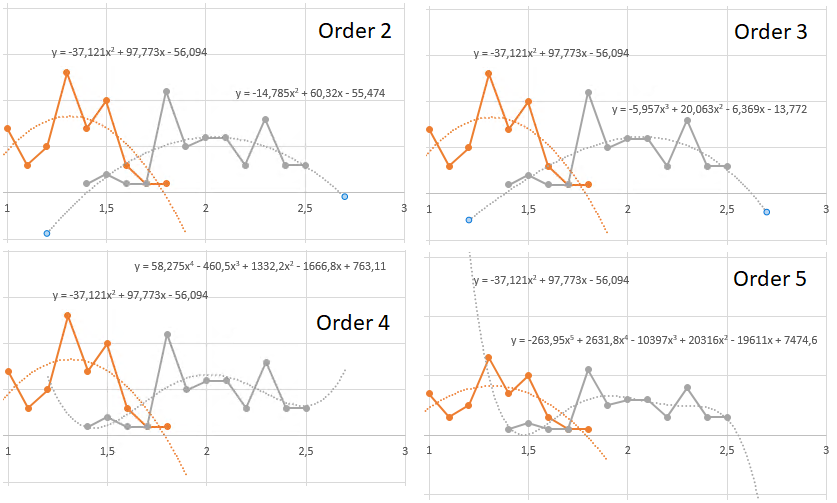
Mais doit-on s'approcher de la réalité et quelles sont les conséquences d'une estimation erronée du nombre d'occurrences des espèces pour une largeur de pétale donnée ? Là encore, il faut mettre en contexte ce qu'on attend. Ce qui nous importe, pour une prise de décision, est la proportion entre les Versicolor et les Virginica. Le nombre d'occurrences estimé n'a aucun intérêt tant que la proportion reste la même. Il y a certainement des théories sur l'ordre à choisir dans un tel cas pour que ces proportions soient correctes mais n'étant pas Mathématicien, je ne les connais pas. Je vais donc essayer de m'approcher le plus possible de la réalité sans avoir à définir l'équation de cette tendance et d'obtenir des proportions "correctes". L'approche va nécessairement avoir des limites.
Pour la largeur des pétales, entre 1.4 et 1.8 cm, nous avons au moins une observable pour chaque milimètre. En outre, les deux courbes se croisent tandis que la première décroit et la seconde croit. Enfin, dans notre approche, nous nous appuyons sur les écarts et sur les observables pour la majorité des réponses. Pour cette dimension, ce sont 5 largeurs sur 17 qui posent questions. Nous ne prenons donc pas grand risque à prévoir le nombre d'occurrence des deux espèces pour 1.55 ou 1.75 par exemple. Il n'en serait pas forcément de même pour la largeur des sépales par exemple.
Nous allons nous appuyer sur les équations des droites entre les points 1.5 et 1.6.
Pour le Versicolor, nous avons une droite y=ax+b entre les points {1.5, 10} et {1.6, 3}. On a donc 10=1.5a+b et 3=1.6a+b b=10-1.5a => 3=1.6a+10-1.5a => 0.1a=-7 => a=-70 et b=115 Pour 1.55 cm nous avons donc 6.5 occurrences.
Pour le Virginica, nous avons une droite y=ax+b entre les points {1.5, 2} et {1.6, 1}. On a donc 2=1.5a+b et 1=1.6a+b b=2-1.5a => 1=1.6a+2-1.5a => 0.1a=-1 => a=-10 et b=17 Pour 1.55 cm nous avons donc 1.5 occurrences.
Pour fournir un ratio le plus correct possible entre Versicolor et Virginica, il semble que nous n'ayons pas intérêt à arrondir ces prévisions. Pour une largeur de 1.5 cm, nous avons 5 fois plus de Versicolor. Pour une largeur de 1.6 cm, nous avons 3 fois plus de Versicolor. Pour une largeur de 1.55 cm, nous aurions 4,33 fois plus de Versicolor. Si on arrondit les prévisions obtenues, nous aurions 3.5 fois plus de Versicolor. Le ratio obtenu à partir de prévisions non arrondies me semble plus exacte. Il en résulte que, dans le code de la classe DataPoint, le paramètre "Y" va devoir accepter des valeurs décimales (être changé en double au lieu d'un integer en C#).
En s'appuyant sur des écarts, des observées et un calcul pour les collisions d'espèces au sein d'écarts, nous avons au moins une limite comparée à une approche ne s'appuyant que sur des tendances : au-delà de nos écarts, nous ne prévoyons rien. Est ce que c'est la bonne approche ? Si nous avions pris la moitié du jeu de données pour l'apprentissage et vérifié les résultats avec la seconde moitié, nous pourrions prédire que nous n'avons pas de réponse en fonction des cas. Tout dépend des valeurs de la moitié du jeu de données utilisé lors de l'apprentissage. Est-ce problèmatique ? Je ne pense pas, à la condition, bien sûr que notre solution ait la capacité de consolider son apprentissage dans le temps, comme nous le faisons. Une solution basée uniquement sur des tendances pourrait fournir des valeurs en dehors de nos écarts mais ils dépendraient beaucoup de l'ordre des tendances calculées. Est-ce qu'elles correspondraient à la réalité est une autre question à laquelle je ne sais pas répondre ...