Sommaire
Neurones numériques et réseaux neuronaux adaptatifs - Réflexion - 29/08/2023
S'il y a une chose que j'ai bien du mal à faire, c'est d'appliquer une méthode sans la comprendre comme d'utiliser une librairie de code sans savoir comment elle fonctionne.
Évidemment on ne peut pas tout comprendre ni réinventer tout ce qui nous entoure mais, il me semble important de s'interroger et d'essayer, à minima, d'en comprendre les grandes lignes.
Ce questionnement incessant permet de remettre en cause certains concepts afin de mieux les appréhender et, de temps en temps, d'aller jusqu'à les remettre en cause.
Aujourd'hui ce qui m'interroge est le fonctionnement des neuronnes numériques, le fonctionnement des réseaux neuronaux, le réglage de leurs paramètres ... bref quelques aspects que j'essaie d'aborder sans prétention et sans savoir jusqu'où cela me mènera.
Ce que je comprends du fonctionnement d'un neurone biologique est assez élémentaire.
Il dispose d'entrées (des dendrites) et d'une ou plusieurs sorties (des axones).
Lorsque la somme du potentiel de ses entrées dépasse son seuil de déclenchement, sa ou ses sorties sont activées.
Au niveau du réseau, les neurones échangent par l'intermédiaire de synapses via des neurotransmetteurs qui sont le "véhicule" inter-synaptique de l'information.
Ce "véhicule" est intéressant car il ne fait pas partie du réseau en tant que tel mais de son environnement.
Cette influence n'est pas claire pour moi mais il semble évident qu'elle impacte la capacité de transmission et qu'elle induit une inertie notamment liée au relâchement des neurotransmetteurs par les synapses.
En s'appuyant sur ces aspects, un neurone numérique dispose:
- d'une collection d'entrées,
- d'une collection de sorties,
- d'un seuil de déclenchement et, pour s'y retrouver lors de sa représentation notamment, d'un identifiant unique.
En numérique, classiquement cet objet s'appelle un "Node".
Les liaisons synaptiques numeriques sont constituées par un autre objet comportant les références aux objets "node" liés et d'un coefficient de transfert.
Le lien est orienté et son identifiant, unique, est constitué de ceux des deux "node" liés.
En numérique, classiquement l'objet de liaison s'appelle un "Edge".
Dans mes premières implémentations, je ne vais pas prendre en compte l'inertie liée au relâchement des neurotransmetteurs par les synapses mais la question reste posée.
Un autre point est de savoir si le coefficient de transfert synaptique peut être supérieur à 1, créant une amplification du signal d'entrée.
J'ai tendance à penser que c'est le cas car le "débit" de l'information de souvenirs renforcés est supérieur à celui de ceux enfouis ... c'est comme si le diamètre de la "tuyauterie" était plus importante pour les usages les plus renforcés.
La propagation d'un signal se fait de proche en proche.
Chaque neurone activé "demande" aux neurones, liés à ses sorties, de recalculer leur signal d'entrée.
Chacun le fait en s'appuyant sur la liste de ses entrées.
Si le seuil de déclenchement est atteint, la propagation continue.
L'ensemble permet donc de créer des graphes orientés.
Comme tout graphe, il y a un risque de boucle infinie qui doit être pris en compte.
J'ignore comment de telles boucles sont gérées dans un cerveau aussi, en attendant d'en savoir plus, le réseau est géré par un objet "controller" qui réagit en atténuant la somme des entrées à chaque rotation.
Inexorablement la somme finie par être inférieure au seuil de déclenchement d'un des neurones de la boucle concernée.
Le "Controller" doit comporter d'autres fonctions comme celle :
- de pouvoir le représenter à tout instant
- de piloter le réseau en mode apprentissage ou opérationnel
- de permettre son renforcement par la détection, en mode opérationnel, de relations de cause à effet.Ce renforcement est réalisé à l'aide d'une liaison directe entre neuronnes.
Passons de la théorie à la pratique avec un premier exemple.
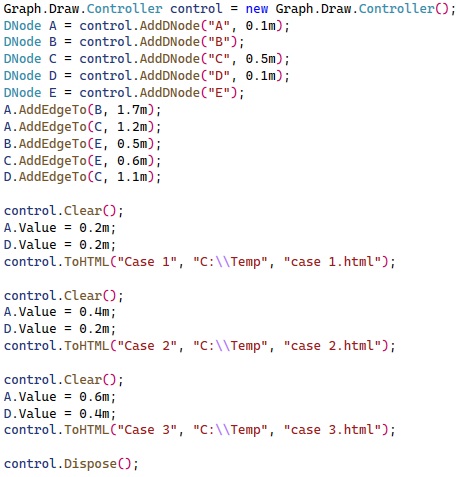
Le code ci-dessous créé un réseau constitué de 5 neurones (A à E), géré par le contrôleur nommé "control".
Le premier paramètre de chaque neurone est son identifiant, le second est son seuil de déclenchement (par défaut 1).
Les relations sont ensuites établies entre les neurones en respectant leur sens et en fournissant leur coefficient d'amortissement\amplification (le "m" caractérise le fait que la valeur est un décimal en langage .Net)
Le sens est important car les réseaux neuronaux sont des graphes orientés.
Les relations entre neurones doivent donc être établies en tenant compte du sens de la propagation du signal.
Les neurones A et D sont les entrées du réseau car ils n'ont pas de neurone associé à leurs dentrites.
Du point de vue biologique ceci n'a aucun sens car tout neurone est forcément associé à une synapse pour recevoir un signal.
Cette synapse peut être associée à un capteur sensoriel par exemple.
Le neurone E est la sortie du réseau car il n'y a aucun neurone associé à son axone.
Du point de vue biologique, là encore, ceci n'a aucun sens car tout neurone est forcément associé à une synapse pour envoyer son signal.
Cette synapse peut être associée à un muscle par exemple.
Dans l'implémentation, le neurone reçoit une valeur s'il n'est associé à aucune forme d'entrée et fourni une valeur s'il n'est associé à aucune forme de sortie.
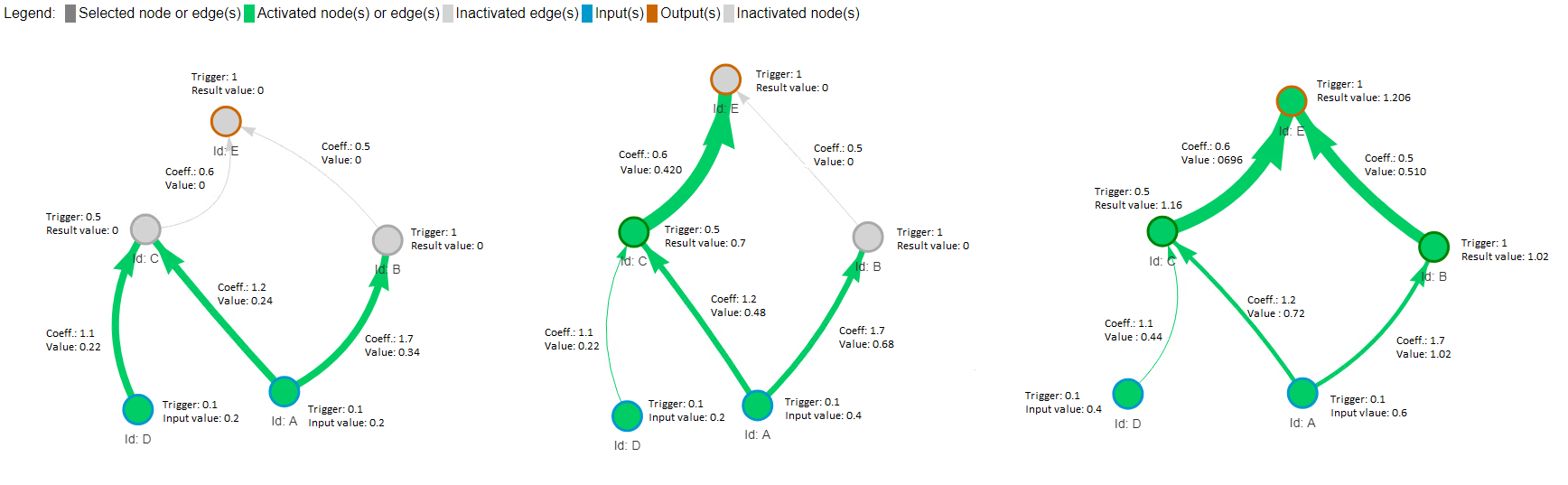
L'image ci-dessous concatène les trois états représentés.
-
Dans le premier cas, les neurones d'entrées ont reçus une valeur d'entrée de 0,2.
Les seuils de déclenchement des neurones C (0.5) et B (1) ne sont pas atteints.
-
Dans le second cas, les neurones d'entrées ont reçus une valeur d'entrée de 0,2 pour D et 0.4 pour A.
Seul le seuil de déclenchement du neurone C (0.5 avec une valeur de 0.7) a été atteint mais ceux de B (1) et E (1) ne sont pas atteints.
-
Dans le troisième cas, les neurones d'entrées ont reçus une valeur d'entrée de 0,4 pour D et 0.6 pour A.
Tous les seuils de déclenchement sont atteints et le neurone E transmet la valeur 1.206 en sortie.
Second exemple avec un convertisseur analogique/numérique
Avec ce second exemple, nous sommes loin de la reconnaissance d'une image ou d'un texte mais l'idée est d'avancer pas à pas.
Cet exemple vise à convertir une valeur d'entrée en son équivalent binaire.
Je suis parti avec une base 2 mais l'approche serait la même pour toute autre base (8, 10, 16 par exemple).
Notre réseau n'a donc qu'une entrée et un nombre de sorties liée à la résolution souhaitée.
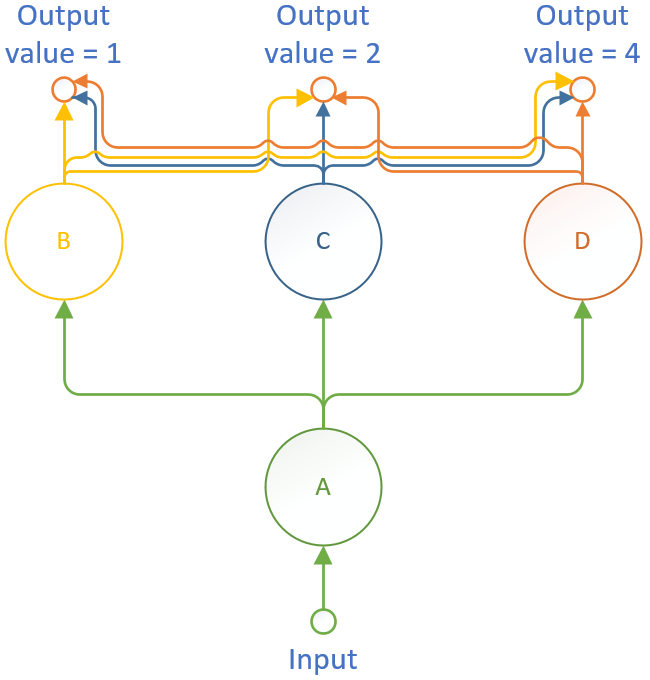
Comment serait structuré le réseau avec l'approche conventionnelle ?
Par convention, tous les neurones d'une couche sont reliés à tous les neurones de la couche supérieure (ou aux sorties).
L'apprentissage supervisé réside dans le fait de déterminer les poids/seuils de chaque liaison/neurone afin d'obtenir les sorties souhaitées.
Le réseau de départ resemblerait à l'image ci-dessous, si tant est que deux couches de neurones suffisent, évidemment.
J'avoue ne pas être "fan" de cette approche qui me semble assez éloignée de la réalité biologique.
J'ai tendance à penser qu'il est préfèrable de partir d'un réseau minimaliste en termes de neurones et de liaisons et de les consolider en fonction des besoins.
J'ignore, bien sûr, si cette approche a pas été prise en compte par le passé et si elle n'aboutit pas à une impasse dans l'état actuel de nos connaissances.
Mais cela ne me gêne pas de me tromper car découvrir et comprendre sont les objectifs premiers de ma démarche.
Je vais donc partir du réseau plus élémentaire ci-dessous et fournir des capacités complèmentaires aux objets en fonction des besoins.
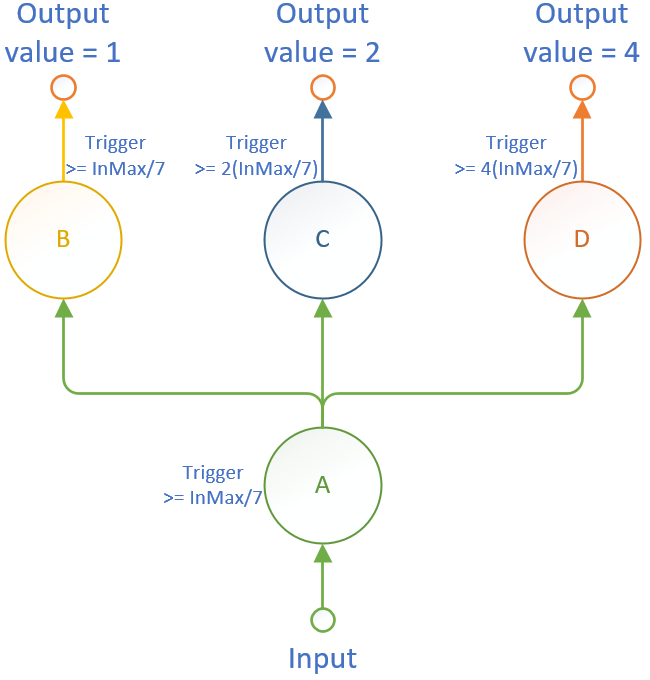
Mon neurone A est l'unique entrée tandis que les neurones B, C et D sont les sorties.
Chacune de ces sorties est censée n'être active qu'en fonction de la représentation binaire de la valeur d'entrée.
Dans la mesure ou je n'ai que trois sorties, je ne vais pouvoir représenter que 8 portions (de 0 à 7) de la valeur d'entrée.
Si la valeur maximale de l'entrée est de 4,9 (volts par exemple - notée InMax), le seuil de A est de 4,9/7 = 0,7 (volt).
Une valeur inférieure est perçue comme 0 avec aucun neurone activé.
Avec un seuil similaire pour B (et une amplification de 1 pour la synapse AB), ma première sortie serait activée en permanence lorsque mon entrée a une valeur comprise entre 0,7 et 4,9.
Un tel comportement ne correspond pas à l'effet souhaité, évidemment.
Je vais donc ajouter une capacité à mes synapses, celle d'être inhibée au-delà d'un seuil.
J'ignore si un tel mécanisme existe dans le biologique mais je n'ai pas de doute sur le fait que notre cerveau soit adaptatif et, dans l'état actuel de nos connaissances, nous ignorons ce qui pilote cette capacité adaptative.
En permettant d'inhiber une synapse, je vais fournir une capacité adaptative au réseau.
Cela va modifier les "opérations mathématiques" et donc les résultats en fonction des entrées.
En définissant la limite de ma synapse AB à 2(InMax/7), elle sera inhibée dès lors que son entrée sera supérieure ou égale 1,4 (volts).
Si le seuil du neurone C est à 2(InMax/7), il sera activé pour toute valeur d'entrée supérieure ou égale à 1,4 (volts).
Nous voyons d'ores et déjà que le problème se déplace au second neurone et ainsi de suite.
Mais comment obtenir que le neurone B soit activé pour une valeur de 3(InMax/7) ?
Apparemment, en ajoutant un neurone intermédiaire, appelé C1, qui s'active pour une entrée supérieur ou égale à 3(InMax/7) et dont la synapse CC1 est inhibée à 4(InMax/7).
De cette façon, le neurone B sera activé pour toute valeur comprise entre 3 incluse et 4 exclue.
Avec cette approche, nous pouvons convertir des valeurs d'entrée de 1 à 4 fois la valeur d'entrée Max/7.
En outre, il m'apparaît important de dicerner les cas ou l'entrée est inférieure à 1(InMax/7) et lorsqu'elle est supérieure à 7(InMax/7).
A défaut, notre réseau fournirait la même valeur de sortie.
Le neurone d'erreur permet donc d'identifier les cas de dépassement de la valeur d'entrée gérée.
La synapse AE n'a pas besoin d'une valeur maximale car la limite d'un décimal est très élevée.
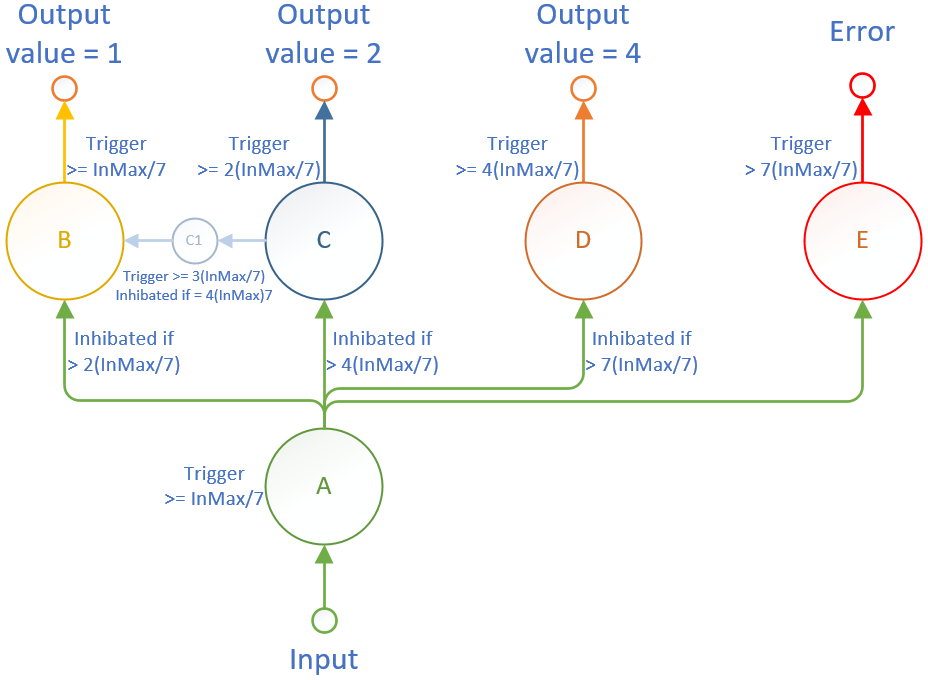
Pour compter au-delà, nous allons devoir ajouter quelques neurones de plus.
Pour une valeur de 5(InMax/7), nous devons activer B et D.
Pour une valeur de 6(InMax/7), nous devons activer C et D.
Pour une valeur de 7(InMax/7), nous devons activer B, C et D.
En somme, pour chaque nouvelle valeur nous devons rajouter un neurone et pour activer plusieurs neurones nous devons ajouter autant de synapses que nécessaires.
Une telle logique est simple à programmer afin de créer un réseau qui permette d'obtenir n'importe quelle résolution de la valeur d'entrée.
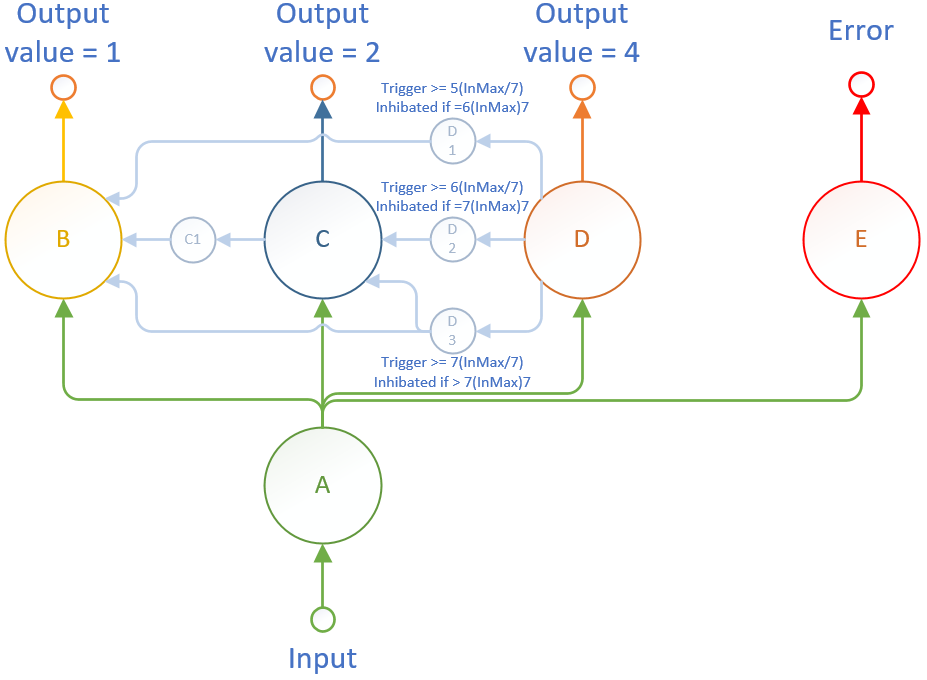
Le neurone D1 est activé pour une valeur d'entrée égale à 5(InMax/7) et sa synapse DD1 limitée à 6(InMax/7).
En s'activant, il active B.
Le neurone D2 est activé pour une valeur d'entrée égale à 6(InMax/7) et sa synapse DD2 limitée à 7(InMax/7).
En s'activant, il active C.
Le neurone D3 est activé pour une valeur d'entrée égale à 7(InMax/7) et sa synapse DD3 limitée à toute valeur supérieure à 7(InMax/7).
En s'activant, il active B et C.
Il nous reste plus qu'à vérifier que les valeurs de seuil des neurones B et C permettent leur activation pour les valeur d'entrée issues de C1, D1, D2 et D3.
Si nous conservons des valeurs d'amortissement/amplification de 1 pour toutes les synapses, nos seuils seront bien dépassés et les sorties activées, ce qui répond à l'objectif.
Par contre, avec une telle approche, les valeurs de sortie seront dépendantes de la valeur d'entrée.
A ce stade, il semble qu'il ne reste plus qu'à modifier le code pour prendre en compte le seuil d'inhibition et s'assurer du fonctionnement de l'ensemble.
Contrôle de la théorie par la mise en pratique.
Après quelques modifications le code fonctionne comme attendu.
Il m'a fallu :
- comme prévu, ajouter le seuil d'inhibition (appelé MaxValue) dans l'objet de liaison (Edge)
- également définir explicitement qu'un neurone est une sortie car les neurones C et D n'étaient plus perçus comme tel du fait de leurs liaisons avec C1, D1, D2 et D3. Ce point posait des problèmes dans les traitements.
- définir la limite de D à 8 (2^3) et non la valeur exacte de 7. Cela implique qu'il aurait fallu tout diviser par 8 et non 7 ... Il en résulte que toute valeur supérieure à 8(InMax/7) entraîne l'activation du neurone E d'erreur.
Une optimisation est à chercher car le calcul de la valeur du neurone B entraîne celle de C1, C, D1, D2, D3 et D et passe de nombreuses fois sur la demande de la valeur de A.
Le réseau neuronal est parcouru de manière réscursive or seuls les neurones d'entrée disposent d'une valeur fixe.
Les autres sont calculés en s'appuyant sur les neurones sources liés et en appliquant les règles.
La représentation graphique entraîne, elle aussi, nécessite un parcours du réseau neuronal.
Résultats pour des valeurs d'entrée de 0 à 2
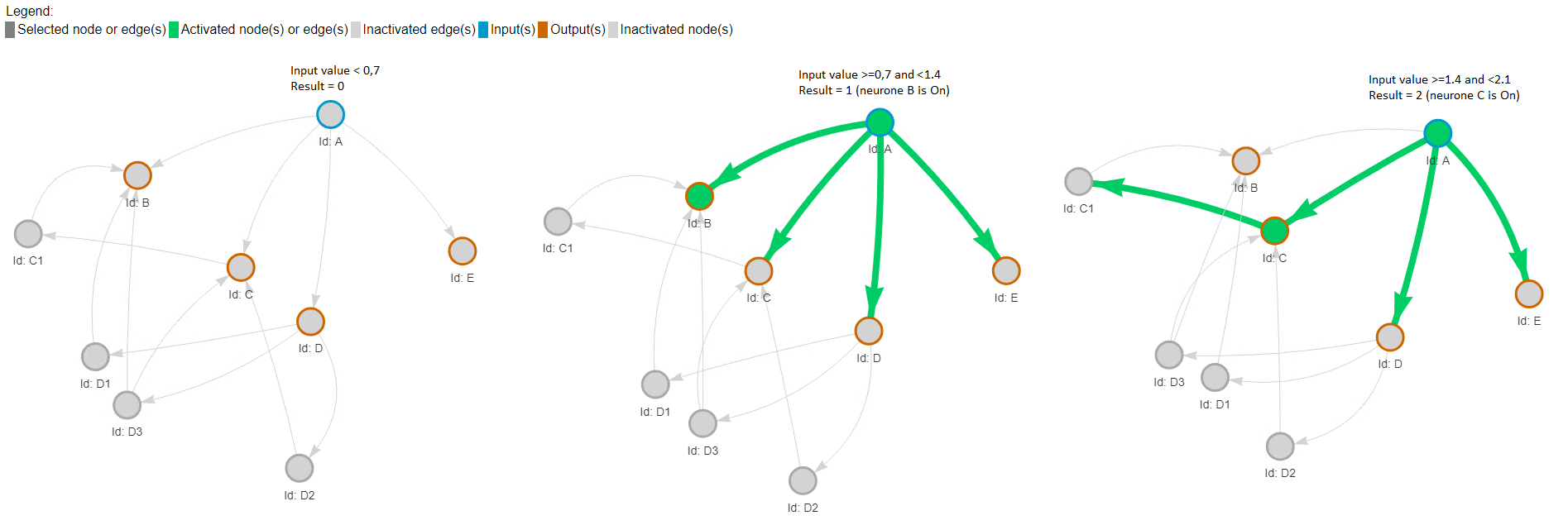
Résultats pour des valeurs d'entrée de 3 à 5
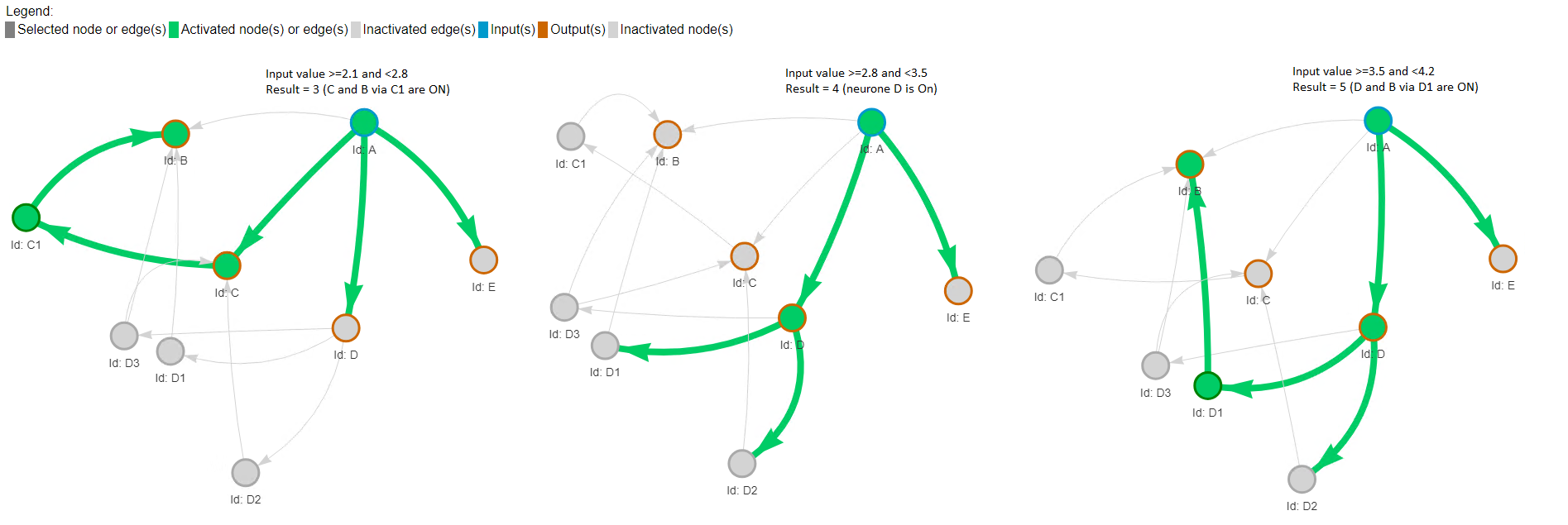
Résultats pour des valeurs d'entrée de 6 à une erreur
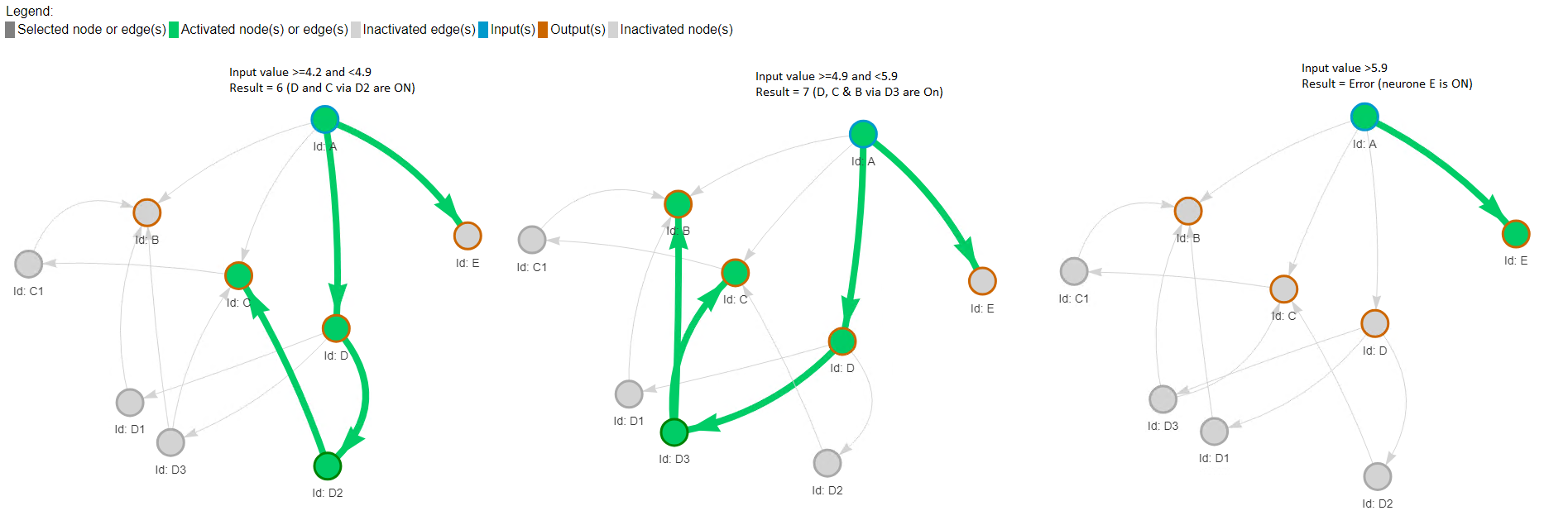
Conclusion
L'exemple démontre que :
- un convertisseur peut être créé à partir d'un réseau neuronal adaptatif.
- le réseau peut être généré et configuré pour toute résolution à partir de règles simples, sans apprentissage.
- la spécialisation des neurones depend des besoins pour plus de simplicité.
L'implémentation actuelle est séquentielle et exécutée dans un seul processus. Cette approche est plus simple et moins coûteuse dans les phases de développement ou pour de petits réseaux.
De réseaux larges necessitent d'être répartis sur plusieurs machines où chaque neurone s'exécute en parallèle.
Ce travail va servir de base à la prochaine réflexion, plus ambitieuse, qui vise à localiser des objets dans des images.
L'objectif est notamment d'identifier leur mouvement dans des séquences.
Références